MDP与蒙特卡洛抽样
2024数模国赛B题第4问|MDP与蒙特卡洛抽样
作者:@同济大学 刘越
Github ID:@miracle-techlink
2024国赛已经匆匆落幕,但是,我们仍然需要总结经验,继续前行。本文将介绍强化学习中的蒙特卡洛方法,并给出一个具体的例子,帮助大家更好地理解这个概念。
在第二问中,因为所有的决策变量都是0-1变量,所以可以使用枚举法,或者蒙特卡洛模拟来求解。第三问,决策空间指数级别上升,暴力求解计算成本过高,所以可以引入启发式算法,比如模拟退火算法,遗传算法,粒子群算法,或者使用特殊的求解器,比如量子计算求解器。但是,在第四问中,决策变量是连续的,所以我们引入了马尔可夫决策过程(MDP),通过MDP根据当前检测结果和历史数据动态调整抽样率,以求的最优解,该方法与蒙特卡洛抽样法相结合,可以有效地解决该问题。
MDP决策推导
马尔可夫决策过程(Markov Decision Process,MDP)是一种用于描述和控制具有不确定性的动态系统的数学模型。它由状态空间、动作空间、转移概率和奖励函数组成。在MDP中,智能体根据当前状态选择动作,并根据转移概率和奖励函数更新状态和奖励。智能体的目标是通过学习最优策略,使累计奖励最大化。
马尔科夫决策过程由元组
:状态空间,表示智能体可能处于的所有状态。 :动作空间,表示智能体可以采取的所有动作。 :转移概率,表示在给定当前状态和动作的情况下,智能体转移到下一个状态的概率。 :奖励函数,表示在给定当前状态和动作的情况下,智能体获得的奖励。 :折扣因子,表示智能体对未来奖励的重视程度。
强化学习的目标是给定一个Markov Decision Process,找到最优策略。最优策略是指状态到动作的映射,常用符号表
给定一个策略
此时
当智能体采取策略
相应地,我们定义状态-行为值函数:
但在实际中,我们无法直接计算
证明过程如下:
对应地,得到状态-行为值函数的贝尔曼方程:
基于蒙特卡洛方法的MDP理论
蒙特卡洛方法原理
我们可以使用动态规划的计算方法来计算期望值,但在没有模型的情况下,我们也可以采用蒙特卡洛方法来估计期望值,即利用随机样本估计期望。其主要思想是利用经验平均代替随机变量的期望值。此处,我们需要理解两个词:经验和平均。
首先,我们来理解什么是“经验”。
当评估智能体当前策略
计算一次试验的回报(return):
其中,
那么,这里,”经验“就是利用该策略做过很多次试验,产生很多幕数据(这里一幕就是一次试验),然后利用这些数据来估计期望值。
接下来,我们理解什么是“平均”。
平均就是利用经验数据来估计期望值。比如,我们利用策略
其中,
每次访问蒙特卡洛方法是指在计算状态s处的值函数时,利用所有访问到状态
在动态规划方法,为保证函数收敛,算法会逐个扫描状态空间中的状态。而蒙特卡洛方法则不需要对状态空间进行扫描,而是通过探索性初始化,即随机初始化状态,然后利用随机策略进行试验,从而产生经验数据,然后利用经验数据来估计期望值。
估计出值函数期望值之后,对每个状态
以及最优策略
$$π_{}(a|s) = \begin{cases}1 & \text{if } a = a_{} \ 0 & \text{otherwise}\end{cases}$$
同时,我们为了设计动态规划方法,我们需要递增计算均值:
接着,我们需要设计探索策略,以便产生经验数据。常用的策略有:
$$π_{\epsilon-soft}(a|s) = \begin{cases}\frac{\epsilon}{|A(s)|} & \text{if } a \neq a_{} \ 1-\epsilon+\frac{\epsilon}{|A(s)|} & \text{if } a = a_{}\end{cases}$$
其中,
由此,我们可以得到蒙特卡洛方法的基本算法流程:
1.初始化值函数
和策略
2.生成一个随机初始状态和一个随机初始动作
3.生成一个随机策略,用于探索状态空间
4.执行动作,观察奖励 和下一个状态
5.对回报值进行取均值,并且对当下策略进行评估
6.对实验中的策略使用 策略进行改进
7.重复步骤2-6,直到达到终止条件
然后,我们再来看国赛B题的具体背景: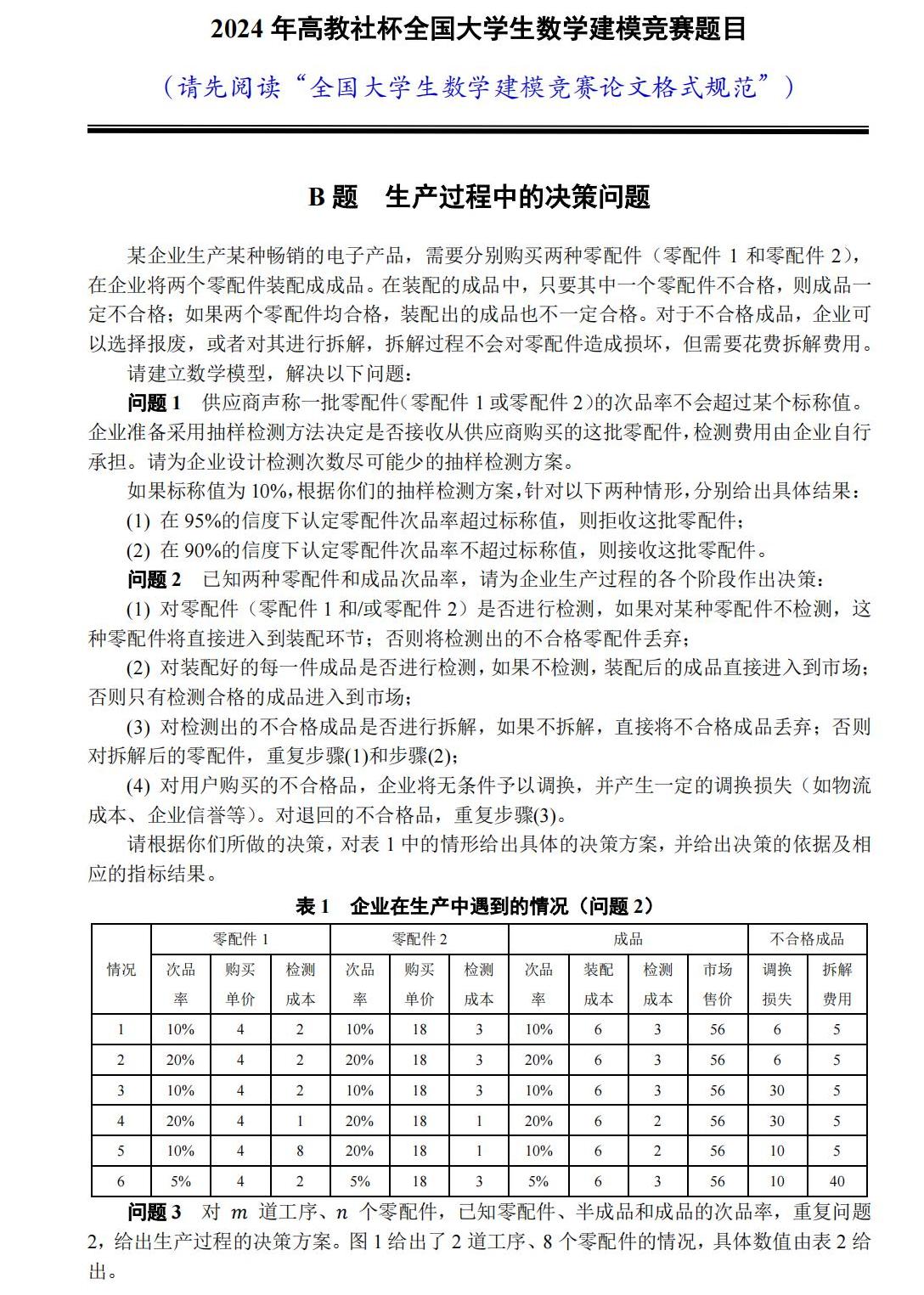
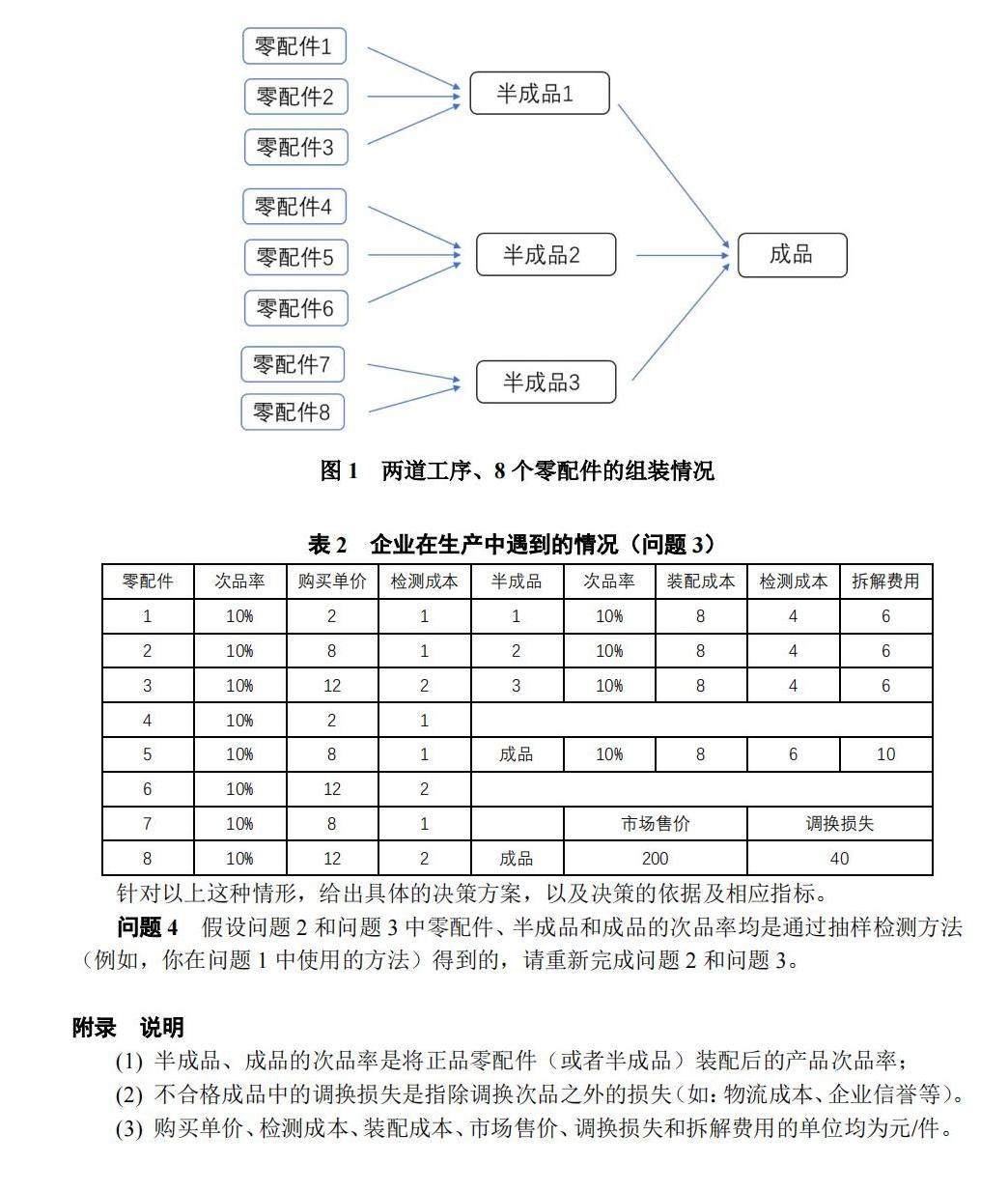
在这题中,蒙特卡洛方法方程可以表示为;