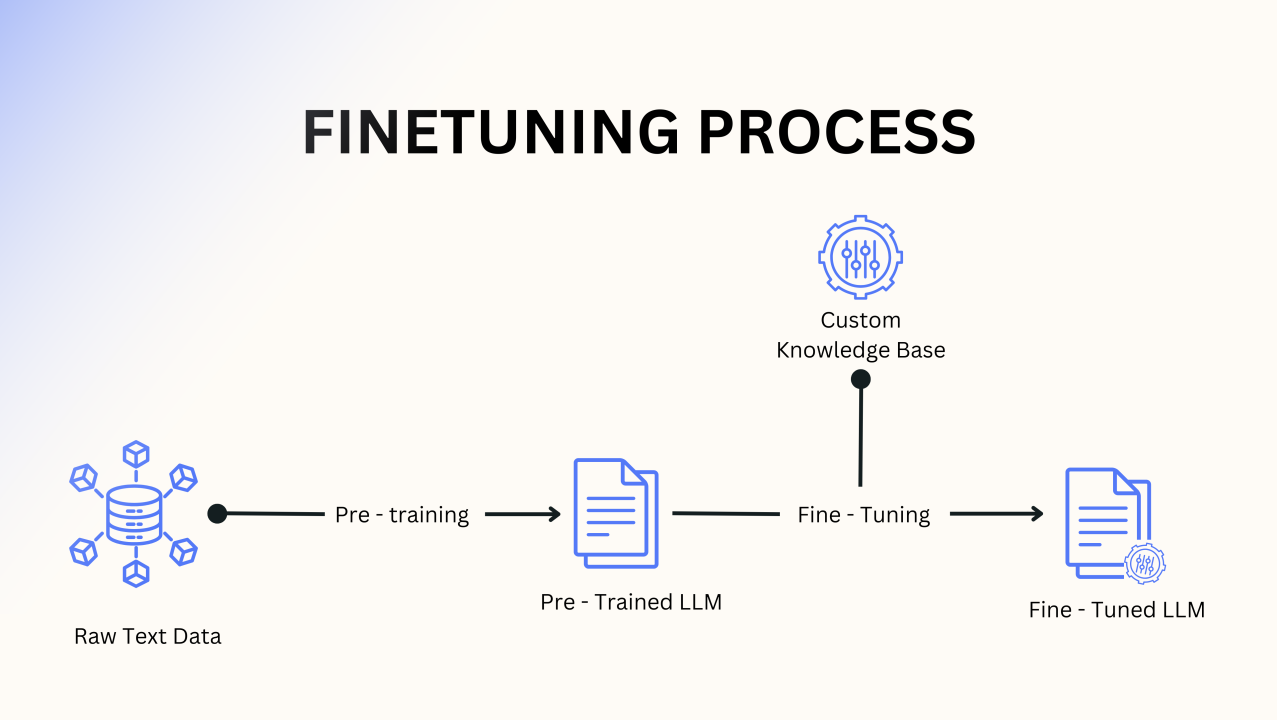
拓扑优化与CFD----高功率芯片设计微流体冷却系统

作者：@同济大学 刘越

Github ID：@miracle-techlink

联系邮箱：miracle.techlink@gmail.com

校内邮箱: 2254018@tongji.edu.cn

引言

注意到，黄大年茶思屋网站中提到了这样一篇文章，《Glacierware: Hotspot-aware Microfluidic Cooling for High TDP Chips using Topology Optimization》,这篇论文是关于高功率芯片设计微流体冷却系统的，于是，我决定写一篇关于拓扑优化与CFD的博客，来记录一下我的学习过程。同时值得注意的是，这项技术目前只有一家瑞士公司（洛桑Corintis公司）已经商业化并且尝试在迁移这套系统的应用场景，希望这篇文章能启发到更多researcher背景的公司创始人。


框架图

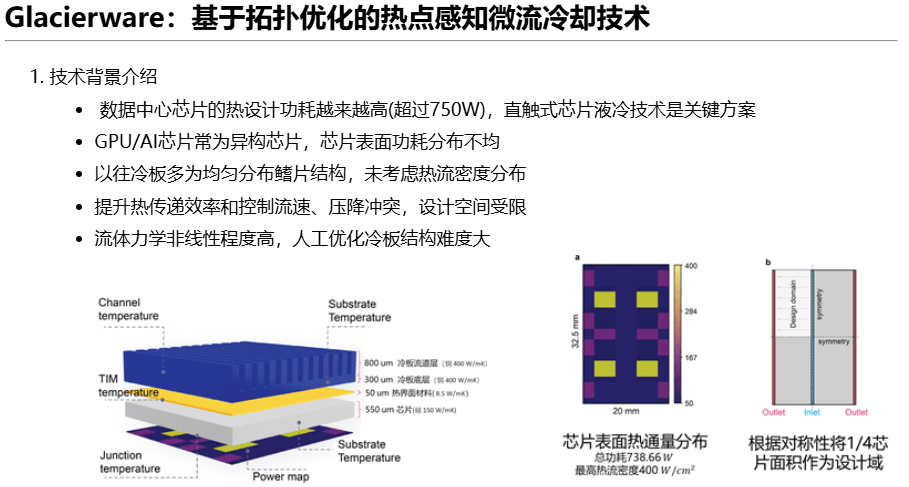
网站页面也给出了这项技术的主要原理和架构图，对于其底层数学的建模原理，我们后续会继续给出分析，而仿真落地的方案因为论文并未开源，目前还在探索过程中，后面有时间才会更新。


框架图

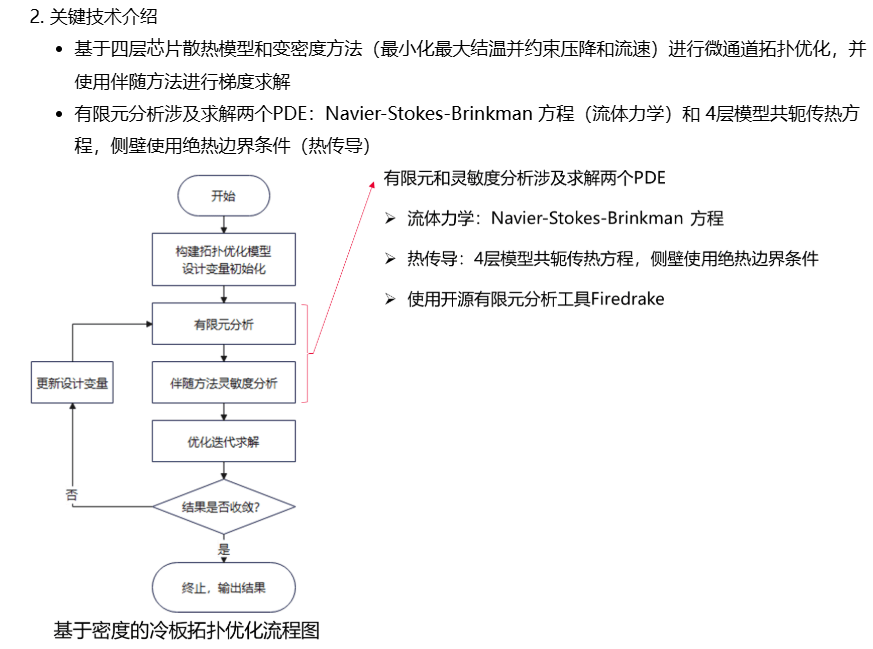
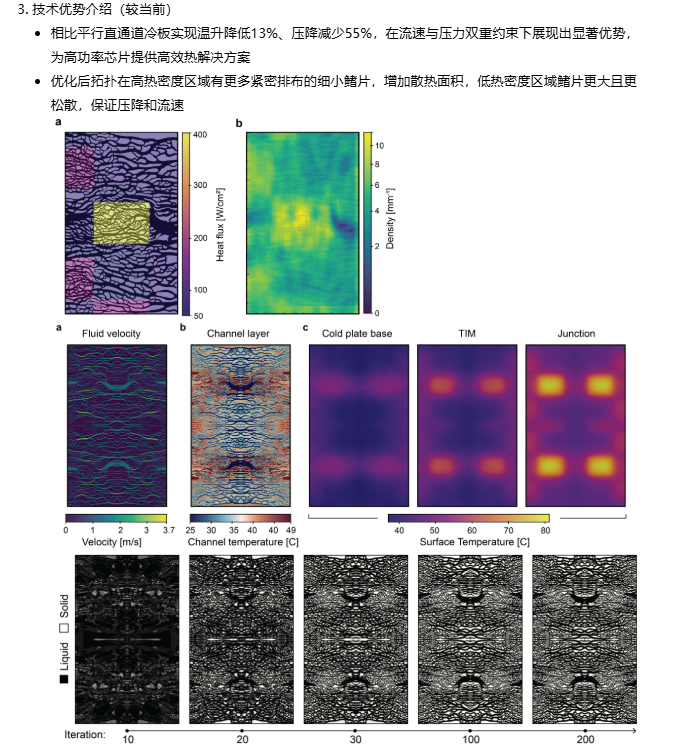
目前这项技术相比平行直通道冷板实现温升降低13%、压降减少55%，在流速与压力双重约束下展现出显著优势，为高功率芯片提供了高效的热解决方案。


框架图


设计变量与拓扑表示

1.设计区域与密度场定义

  • 设计区域（设计域）记作 ，其边界为 。

  • 密度场 ，称为设计变量。

    • 通常取 （或更小），以保证刚度矩阵良好条件数。
    • 表示该处有材料， 表示该处几乎无材料（但保留一点避免计算奇异）

  • 阈值映射（最终材料分布）:设定一个标准阈值 ，把密度场二值化：

  • 为什么用密度场？

    1. 传统设计是“材料有或没有”（0 或 1），直接优化 0–1 会导致计算困难；
    2. 用连续的密度场（0 到 1 之间平滑变化）代替，方便数值处理；
    3. 最后再通过“阈值”转化为 0–1 分布，实现清晰的最终结构。

2.SIMP 惩罚插值模型

在基于密度的拓扑优化里，我们需要把“要不要放材料”这个二值决策（0 或 1）转换成连续变量，以便用梯度方法来求解。SIMP（Solid Isotropic Material with Penalization）模型，就是用来做这个“插值＋惩罚”的一套简单而有效的方法。

  1. 连续密度变量
    我们不直接让每个单元要么“实心”（密度为1），要么“空心”（密度为0），而是允许它在 之间平滑变化：

  2. 刚度与密度的关系
    如果把单元想象成“橡皮糖”，密度越高就越“硬”。我们用数学公式把刚度（杨氏模量 ）和密度 联系起来：

    其中

    • 是纯材料的刚度（当 时的杨氏模量），
    • 指数 是“惩罚因子”，通常取 或 。

  3. 为什么要惩罚？

    • 如果 ，那就是线性插值， 时，单元刚度刚好是一半——中间态并不“吃亏”。
    • 当我们把 调大（比如 ），就会让中间密度的单元“变得很软”——远远低于线性插值的硬度。这样，优化过程中那些“半实心”单元会被驱动更快地向 0 或 1 收敛，最后结构才更清晰可制造。

  4. 单元刚度矩阵的表达
    在有限元计算里，每个单元都有一个刚度矩阵 ，代表“实心材料时”的力学响应。加上 SIMP 插值后，就变成：

    • 当 （实心）时，。
    • 当 （空心）时，，相当于“拿掉”这个单元。

    这样就把“材料分布”问题，转化为一个连续优化问题，又保证最后得到的结构足够“二值化”，便于后续加工和打印。

3.Helmholtz 滤波 —— 平滑与最小特征尺寸保障

在优化迭代中，未经处理的密度场往往会出现“棋盘格”伪影或过细结构。Helmholtz 滤波就是在每步迭代前，通过解线性方程组在“恢复原始密度分布”与“空间平滑”之间取得平衡，相当于对原始密度 做一次平滑，得到用于优化的 。想象往密度图上盖一层软化剂，把“小桥”、“小岛”都抹平，留下足够宽度的通道或梁。滤掉小于 尺度的噪声特征，防止结构过细、易断。这样使得后续灵敏度计算更平滑，算法更稳健。

  1. 滤波方程

    • ：优化器输出的“原始”密度
    • ：平滑后的密度，送入物理分析
    • ：滤波半径，决定“抹平”范围，也对应了最小特征宽度

  2. 有限元离散
    在实际数值中，上式被写成矩阵形式：

    • ：质量矩阵；：Laplace（离散拉普拉斯）矩阵；：单元或节点上的密度向量
    • 就相当于在“还原原始信息”和“空间平滑”之间做一个最优折中，得到既保留全局分布趋势、又去除微小噪声的平滑密度场。

4.密度场初始化 —— 均匀探测 vs.经验引导

拓扑优化前要给每个单元一个初值 ，好比在空白画布上先定下颜色基调。密度场初始化则是在优化开始前给每个单元指定一个合理的初始密度分布。最常用的均匀体积分数初始化保证了全局无偏搜索，而基于参考设计的混合初始化则通过一个权重参数兼顾先验经验和全局探索，能够在一定程度上加速收敛并避免局部最优。

  1. 均匀体积分数

    • 是目标体积分数（例如 0.5），表示整体“材料覆盖率”。

  2. 经验布局叠加

    • ：已有的参考设计密度场
    • ：权重，决定对参考设计的信任程度

以上两个步骤——Helmholtz 滤波与密度场初始化——是保证拓扑优化过程中结构可制造性、数值稳定性和收敛效率的关键前处理。

物理场约束（PDE 建模）

下面对“流固耦合（Navier–Stokes–Brinkman）”及“共轭传热”两部分做数学推导与通俗解读。

1. 流固耦合（Navier–Stokes–Brinkman）

我们把设计域看作一个“多孔介质”，用 Brinkman 项在流动方程中惩罚“固体”区域中的速度，从而将流体与结构耦合。

1. 基本方程

动量方程（Navier–Stokes–Brinkman）

其中:

  • ：速度场
  • ：压强
  • ：流体密度
  • ：动力粘度
  • ：Brinkman 惩罚系数，用设计变量 定义
  • ：体力（如重力）

连续性方程（不可压缩条件）

2. Brinkman 惩罚项

  • 在“固体”处我们希望速度趋于零，于是定义

    其中
    • ：最大惩罚系数
    • ：惩罚指数
    • （纯流体）时，；（几乎固体）时，

3. 弱形式及有限元离散

对动量方程乘以试函数 并在域 上积分，施加无滑移或给定边界条件后有：

$$
\begin{aligned}\int_\Omega \rho_f\Bigl(\frac{\partial \mathbf{u}}{\partial t} + \mathbf{u}\cdot\nabla\mathbf{u}\Bigr)\cdot\mathbf{v},\mathrm{d}x

  • \int_\Omega 2\mu,\boldsymbol\varepsilon(\mathbf{u}):\boldsymbol\varepsilon(\mathbf{v}),\mathrm{d}x \
    \quad + \int_\Omega \alpha(\rho),\mathbf{u}\cdot\mathbf{v},\mathrm{d}x
  • \int_\Omega p,\nabla\cdot\mathbf{v},\mathrm{d}x
    = \int_\Omega \mathbf{f}\cdot\mathbf{v},\mathrm{d}x,
    \end{aligned}
    $$

并配合

作为压力试函数 的约束。离散后得到矩阵方程：

  • ：质量矩阵
  • ：对流项刚度矩阵
  • ：粘性项刚度矩阵
  • ：Brinkman 惩罚矩阵，依赖设计变量
  • ：离散化的散度矩阵

2. 共轭传热（Conjugate Heat Transfer）

在多层结构中，需要同时考虑固体的热传导与流体的对流换热，并在两者界面上做温度和热通量连续。

1. 固体区热传导方程

  • ：固体温度
  • ：固体密度
  • ：固体比热容
  • ：固体热导率
  • ：固体内部热源密度

2. 流体区热对流方程

  • ：流体温度
  • ：流体比热容
  • ：流体热导率
  • ：流体内部热源密度（通常取 0）

3. 界面连续条件

在固—流两相交界面 上，要求温度和法向热通量连续：

4. 弱形式及离散

将固体和流体的热方程分别作加权残量并积分，合并界面条件后，离散成一组耦合的矩阵方程：
$$

,
$$
并在组装时对交界面单元添加耦合刚度来保证温度与热通量的连续。

解读要点

  1. 流固耦合：通过在动量方程中引入 惩罚项，把固体区域“堵死”成多孔介质，实现结构与流体的自洽耦合。
  2. 共轭传热：在固体内部用纯热传导方程，在流体中加入对流项，两者用界面温度与热通量连续条件耦合，保证热场的一致性。
  3. 有限元离散：分别对动量-连续性方程和热方程作弱形式、网格离散，得到依赖设计变量 的耦合矩阵方程，用于拓扑优化迭代中的物理场求解。