Miracle Techlink

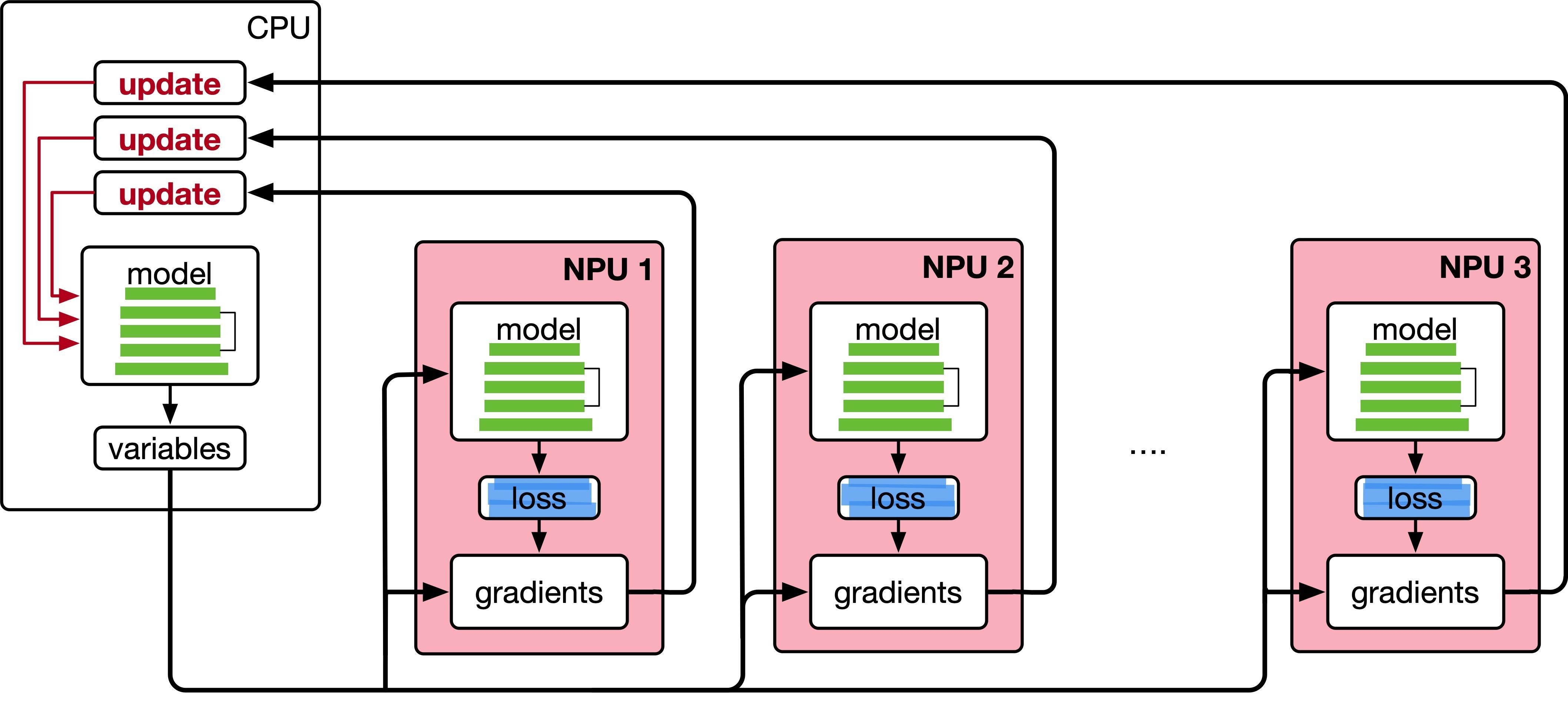
LLM分布式训练1---基础知识篇 作者：@同济大学 刘越 Github ID：@miracle-techlink 联系邮箱：miracle.techlink@gmail.com 校内邮箱: 2254018@tongji.edu.cn 引言随着大语言模型参数量和所需训练数据量的急速增长，单个机器上有限的资源已无法满足其训练的要求。需要设计分布式训练系统来解决海量的计算和内存资源需求问题。在分布式训练系统环境下，需要将一个模型训练任务拆分成多个子任务，并将子任务分发给多个计算设备，从而解决资源瓶颈。如何才能利用数万个计算加速芯片的集群，训练千亿甚至万亿个参数量的大语言模型?这其中涉及集群架构、并行策略、模型架构、内存优化、计算优化等一系列的技术。 本章将介绍分布式机器学习系统的基础概念、分布式训练的并行策略、分布式训练的集群架构，并以 DeepSpeed 为例，介绍如何在集群上训练大语言型。而这篇推送将主要介绍分布式训练的基础概念。 分布式机器学习系统的基础概念 分布式训练的并行策略 分布式训练的集群架构 实操DDP-以DeepSpeed 为例 ...

2024数模国赛B题第4问|MDP与蒙特卡洛抽样 作者：@同济大学 刘越 Github ID：@miracle-techlink 联系邮箱：miracle.techlink@gmail.com 2024国赛已经匆匆落幕，但是，我们仍然需要总结经验，继续前行。本文将介绍强化学习中的蒙特卡洛方法，并给出一个具体的例子，帮助大家更好地理解这个概念。 在第二问中，因为所有的决策变量都是0-1变量，所以可以使用枚举法，或者蒙特卡洛模拟来求解。第三问，决策空间指数级别上升，暴力求解计算成本过高，所以可以引入启发式算法，比如模拟退火算法，遗传算法，粒子群算法，或者使用特殊的求解器，比如量子计算求解器。但是，在第四问中，决策变量是连续的，所以我们引入了马尔可夫决策过程（MDP），通过MDP根据当前检测结果和历史数据动态调整抽样率，以求的最优解，该方法与蒙特卡洛抽样法相结合，可以有效地解决该问题。 MDP决策推导马尔可夫决策过程（Markov Decision Process，MDP）是一种用于描述和控制具有不确定性的动态系统的数学模型。它由状态空间、动作空间、转移概率和奖励函数组成。在MDP中， ...

AI+math|从Alphafold说起 引言 作者：@同济大学 刘越 Github ID：@miracle-techlink 联系邮箱：miracle.techlink@gmail.com 校内邮箱: 2254018@tongji.edu.cn 特别感谢以下组织和个人提供的帮助：Datawhale开源学习社区 （点击链接进入其github教程仓库）集智俱乐部(https://pattern.swarma.org/user/116904) (点击链接进入官网)@同济大学数学科学学院陈小杨教授 （邮箱：xychen100@tongji.edu.cn） 2024年诺贝尔化学奖授予大卫·贝克（David Baker）、戴米斯·哈萨比斯（Demis Hassabis）和约翰·江珀（John M.Jumper），以表彰他们在蛋白质设计和蛋白质结构预测领域作出的贡献。他们与Deepmind公司在2020年发布的lphaFold2算法，在蛋白质结构预测领域取得了重大突破，其预测结果与实验结果高度一致，为生物科学领域带来了革命性的影响。我们今天就一起走进AlphaFold的世界，了解其背后的原理 ...

如何科学绿色上网|clash安装教程 引言 作者：@同济大学 刘越 Github ID：@miracle-techlink 联系邮箱：miracle.techlink@gmail.com 校内邮箱: 2254018@tongji.edu.cn Clash for Windows 是代理工具Clash在Windows系统的图形客户端，同时还支持Linux、macOS系统，功能强大且支持多种代理协议，如V2Ray、Trojan、Shadowsocks(R)、Socks等协议。 2023年11月2日Clash for Windows作者Fndroid删除了该项目GitHub仓库并宣布停更，原因未知（进去坐大牢了），但已发布版本均正常可用。 clash项目是完全免费的，但是其缺点也显而易见，由于缺乏足够人手维护，虽然一直以来没有出现过问题，不过稳定性还是被人所质疑。 如果大家对其安装或者使用不是很有信息，就使用Sakuracat(下载链接)。每月10块不到，就可以享受非常稳定的代理服务。不过由于其没有全局代理服务，无法登录使用GPT等需要全局代理的网站。 一.下载 ...

Datwhale|力扣刷题之枚举算法 作者：@同济大学 刘越 Github ID：@miracle-techlink 联系邮箱：miracle.techlink@gmail.com 本文为Datawhale组队学习之Leetcode刷题笔记，感谢Datawhale提供的学习资源以及组队学习的小伙伴们的讨论与帮助。 本文教程链接如下：Github地址 PS: 原教程使用python编写，而本文使用C++语言。 枚举算法简介枚举算法的核心思想是：通过列举问题的所有状态，将它们逐一与目标状态进行比较，从而得到满足条件的解。 由于枚举算法要通过列举问题的所有状态来得到满足条件的解，因此，在问题规模变大时，其效率一般是比较低的。但是枚举算法也有自己特有的优点： 多数情况下容易编程实现，也容易调试。 建立在考察大量状态、甚至是穷举所有状态的基础上，所以算法的正确性比较容易证明。 所以，枚举算法通常用于求解问题规模比较小的问题，或者作为求解问题的一个子算法出现，通过枚举一些信息并进行保存，而这些消息的有无对主算法效率的高低有着较大影响。 枚举算法的解题思路枚举算法解题步骤采用枚举算法解题的 ...